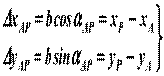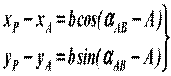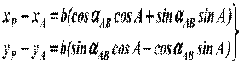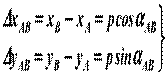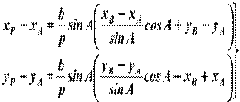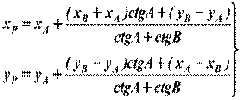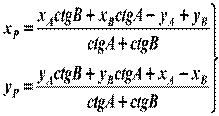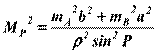Прямая угловая засечка

Здравствуйте, уважаемые читатели моего блога!

Для того, чтобы научиться выполнять элементарные геодезические работы, требуется освоить основные способы разбивки на местности.

Там, где разбивка точек невозможна из-за их недоступности, а также значительном расстоянии от исходных пунктов, применяется прямая угловая засечка (также существует обратная и линейная засечки). Что представляет собой этот способ, узнаем ниже.

 

 

 

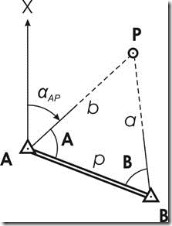
Рисунок 1.

На рис.1 представлена схема прямой однократной засечки (бывают многократные). Здесь А и В – исходные, с прямой видимостью, а точка Р – определяемая. Внутренние углы полученного треугольника А и В измерены. Исходные координаты обозначаем, как Ха, Уа, Хв, Ув, определяемая точка Р, соответственно, Хр, Ур. Далее, согласно формуле:

(1.1)

Дирекционный угол αАВ определяется, как разность:

(1.2)

Угол αАВ можно найти с помощью решения обратной геодезической задачи, зная исходные координаты А и В. Подставляем 1.2 в 1.1:

(1.3)

Другой вариант:

(1.4)

Приращения координат: ∆х АВ, ∆у АВ:

(1.5)

Откуда следует:

(1.6)

Продолжаем вычисления, вставив 1.6 в 1.4, получаем:

(1.7)

Рассмотрев треугольник АВР, считаем:

(1.8)

Умножаем части равенства 1.8 на sin А. Результат:

(1.9)

Далее делим числитель и знаменатель правой части формулы 1.9 на —

(1.10)

Ставим данные 1.10 в 1.7, преобразовываем и получаем:

(1.11)

Написанные выше формулы выполнены для угла А. Для В – аналогичные расчеты. Формулы 1.11 иногда даются в другом варианте:

(1.12)

Это и есть формулы Юнга или формулы котангенсов. При их использовании соблюдается следующий порядок по пунктам:

— Р – определяемый,

— А – левый исходный,

— В – правый исходный,

— стоя со стороны АВ лицом к точке Р, углы находятся при А и В.

Часто задаётся вопрос: какова точность определения координат Р? Ответ таков: квадрат средней квадратической погрешности вычисляется по формуле:

(1.13)

Погрешность – Мр2.

mA, mB – средние квадратические погрешности А, В.

а и b – противолежащие внутренним углам А, В стороны треугольника АВР.

Р – внутренний угол при точке Р. Число секунд в радиане:

Значение этого числа нужно брать в соответствии с mA, mB. Углы А, В, как правило, измеряются равноточно, поэтому записываем: mA=mB=mβ. Затем принимаем обозначения – а=s1, в=s2 , после чего формулу 1.13 можно представить по-другому:

(1.14)

Учитывая следующие равенства:

(1.15),

получаем: (1.16)

Формулы оценки точности 1.14 и 1.16 показывают увеличения средней квадратической погрешности определяемого пункта, в связи с удалением её от исходных пунктов, а также увеличением базиса засечки (Р). Чем ближе к 90 градусам угол засечки Р, тем меньше погрешность вычислений.

На этом все друзья. Спасибо за внимание. Отличного Вам дня и хорошего настроения. Пока!!